FUNDAMENTOS DE ELECTRICIDAD
SECCIÓN 1.2
Visite su biblioteca local y mencione que tanta información y qué tipos de apoyo hay sobre la computación aplicada a las tecnologías en particular: la electricidad, la electrónica, la electromagnética y las computadoras.
La universidad Anáhuac de Xalapa cuenta con una biblioteca la cual posee un gran número de documentos y videos relacionados con la electricidad, la electrónica, la electromagnética y las computadoras. Incluso la Universidad cuenta con un área de especialización llamada Ingeniería en Tecnologías Estratégicas de la Información dedicada al estudio, manejo y manipulación tecnológica.
Actualmente cuenta con laboratorios de cómputo, electricidad, física, los cuales están divididos para mayor comodidad.
Seleccione un área de interés particular en este campo y escriba un informe breve de la historia del tema.
La electricidad es la categoría de fenómenos físicos originados por la existencia de cargas eléctricas por la interacción de las mismas. Cuando una carga eléctrica se encuentra estacionaria o estática, produce fuerzas eléctricas sobre las otras situadas en su misma región del espacio, cuando esta en movimiento, produce además efectos magnéticos.
Los efectos eléctricos y magnéticos dependen de la posición y movimientos relativos de las partículas con carga. En lo que respecta a los efectos eléctricos, estas partículas pueden ser neutras positivas o negativas.
La electricidad se ocupa de las partículas cargadas positivamente, como los protones que se repelen mutuamente, y de las partículas cargadas negativamente, como los electrones, que también se repelen mutuamente. En cambio las partículas negativas y positivas se atraen entre sí.
SECCIÓN 1.3
Determine la distancia en pies que recorre en un minuto un auto que avanza a 50 mi/h.
1 milla = 5280 pies. 1 milla ---- 5280 pies. 264,000 pies ---- 60 minutos.
1 milla = 1/60 horas. 50 millas ---- X= 264,000 pies. X= 4,400 pies ---- 1 minuto.
Recorre 4,400 pies en un minuto.
¿Cuántas horas necesita una persona para recorrer 12 mi a una velocidad promedio de 15 minutos/milla?
15 minutos ---- 1 milla. 1 hora ---- 60 minutos Necesita 3 horas.
X=180 minutos ---- 12 millas. X= 3 ---- 180 minutos
SECCIÓN 1.4
¿Cuántas pies - libras de energía se asocian con 1000J?
1 Joule ---- .7376 pies/libra.
1000 J ---- X= 737.6 pies/libra.
¿Cuántos centímetros hay en 1/2 yardas?
1 metro ---- 1.093 yardas 1/2 yarda = .5465 1 metro ---- 100 centímetros.
.5465 metros ---- X= 54.65 centímetros.
SECCIÓN 1.6
Exprese los siguientes números como potencias de 10.
a) 10,000 = 1X104 b) 0.0001 = 1X10-4 c) 1000 = 1X103 d) 1,000,000 = 1X106
e) 0.0000001 = 1X10-7 f) 0.00001 = 1X10-5
Usando solo las potencias de diez exprese los números siguientes en la forma que considere más lógica para cálculos posteriores.
a) 15,000 = 15X103 b) 0.03000 = 3X10-2 c) 7,400,000 = 74X105 d) 0.0000068 = 6.8X10-6
e) 0.00040200 = 4.02X10-4 f) 0.0000000002 = 1X10-10
SECCIÓN 1.7
Complete los espacios en blanco en las conversiones siguientes.
a) 6X103 = 0.006000X106 b) 4X10-4 = 400X10-6 c) 50X105 = 500X103 = 0.5X10-6 = 0.0005X109
d) 30X10-8 = 0.000030X10-3 = 3000X10-6 = 3000X10-9
Lleve a cabo las conversiones siguientes:
a) 2000 microsegundos a milisegundos.
(2000X10-6)(1X10-3) = 2X10-6
b) 0.04 milisegundos en microsegundos.
(0.04X10-3)/(1X10-6) = 4X10-11
c) 0.06 micro Farads en nanoFarads.
(0.06X10-6)/(1X10-9) = 60 nanoFarads.
d) 8400 picosegundos en microsegundos.
(8400X10-12)(1X10-6) = 8.4X10-15
e) 0.006 Kilómetros en milímetros.
1 kilómetro ---- 100,000 milímetros.
0.006 Kilómetros ---- X= 600 milímetros.
f) 260X103 milímetros en kilómetros.
1 Kilómetro ---- 100,000 milímetros.
X= 2.6 Kilómetros ---- 260X103 milímetros.
SECCIÓN 1.8
a) 1.5 minutos en segundos.
1 minuto ---- 60 segundos
1.5 minutos ---- X= 90 segundos.
b) 0.04 horas en segundos
1 hora --- 60 minutos
0.04 horas ---- X= 2.4 minutos.
c) 0.05 segundos en microsegundos.
(0.05)(1X10-6) = 5X10-8
d) 0.16 metros en milímetros.
1 metro ---- 100 centímetros 1 centímetro ---- 10 milímetros
.16 metros ---- X= 16 centímetros 16 centímetros ---- X= 160 milímetros.
e) 0.00000012 segundos nanosegundos
(1.2X10-7)(1X10-9) = 1.2X10-16
f) 3620000 segundos en días.
3620000/60/60/24 = 41.898 días.
g) 1020 milímetros en metros.
1 metro ---- 1000 milímetros
X= 1.02 metros ---- 1020 milímetros.
Realizar las siguientes conversiones.
a) 0.1 microfarads en picofarads.
(0.1X10-6)/(1X10-12) = 1,000,000.
b) .467 kilómetros en metros
1 kilómetros ---- 1000 metros
.467 kilómetros ---- X= 467 metros.
c) 63.9 milímetros en centímetros.
1 centímetro ---- 10 milímetros
X= 6.39 centímetros ---- 63.9 milímetros.
d) 69 centímetros en kilómetros.
1 kilómetros ---- 100,000 centímetros.
X= 6.9 X10-4 ---- 69 centímetros.
e) 3.2 horas en milisegundos.
(3.2)(1X10-3) = 3.2X10-3
f) 0.016 milímetros en micrómetros.
(0.016)/(1X10-6) = 16,000 micrómetros.
g) 60 cm2 en m2.
1 m2 ---- 10 000 cm2
X= 6X10-3 m2 ---- 60 cm2
SECCIÓN 1.10
a) segundos en 1.4 días.
1 hora ---- 3600 segundos. 1 día ----- 86,400 segundos
24 horas ---- 86,400 segundos. 1.4 días ----- X= 120,960 segundos.
SECCIÓN 1.11
Investigue la disponibilidad de cursos de computación y el tiempo que he dedicado a esta área de su formación como profesionista ¿Cuáles lenguajes emplean comúnmente y que software es popular?
La Universidad Anáhuac se ha preocupado por crear profesionistas que tengan un amplio conocimiento de las herramientas computacionales, y de otros dispositivos que puedan facilitar el trabajo de sus egresados.
Existen un gran número de lenguajes de programación entre los cuales destacan, Pascal, C, C++, Visual Basic, Java, entre otros. Los software son paquetería de office, programas de dibujo como Autocad entre otros.
Elabore una lista de cinco lenguajes populares de computadora y por qué considera usted que algunos lenguajes son mejores que otros para el análisis de circuitos eléctricos?
Los lenguajes de programación ya han sido mencionados en la pregunta anterior, y la diferencia radica principalmente en la facilidad del manejo de lenguajes de programación.
INVESTIGACIÓN ACERCA DE EL VOLTAJE
1. ¿Qué es el voltaje?
El voltio es la unidad SI de diferencia de potencial y se define como la diferencia de potencial que existe entre dos puntos cuando es necesario realizar un trabajo de 1 julio para mover una carga de 1 culombio de un punto a otro.
El potencial eléctrico esta relacionado con la energía potencial Eléctrica. Por ejemplo supongamos que en un sistema existen dos objetos cargados, A y B, si B se acerca a A, la energía potencial cambia. El cambio de la energía potencial es igual a la carga de B, multiplicada por la diferencia de potencial eléctrico entre las posiciones iniciales y final de B.
2. ¿En qué unidades se mide el voltaje?
El voltaje según el Sistema Internacional se mide en Voltios o Volts. El instrumento más utilizado para medir la diferencia de potencial (el voltaje) es un galvanómetro que cuenta con una gran resistencia unida a la bobina. Cuando se conecta un medidor de este tipo a una batería o a dos puntos de un circuito eléctrico con diferentes potenciales pasa una cantidad reducida de corriente (limitada por la resistencia en serie) a través del medidor. La corriente es proporcional al voltaje, que puede medirse si el galvanómetro se calibra para ello. Cuando se usa el tipo adecuado de resistencias en serie un galvanómetro sirve para medir niveles muy distintos de voltajes. El instrumento más preciso para medir el voltaje, la resistencia o la corriente continua es el potenciómetro, que indica una fuerza electromotriz no valorada al compararla con un valor conocido. Para medir voltajes de corriente alterna se utilizan medidores de alterna con alta resistencia interior, o medidores similares con una fuerte resistencia en serie.
Los demás métodos de medición del voltaje utilizan tubos de vacío y circuitos electrónicos y resultan muy útiles para hacer mediciones a altas frecuencias. Un dispositivo de este tipo es el voltímetro de tubo de vacío. En la forma más simple de este tipo de voltímetro se rectifica una corriente alterna en un tubo de diodo y se mide la corriente rectificada con un galvanómetro convencional. Otros voltímetros de este tipo utilizan las características amplificadoras de los tubos de vacío para medir voltajes muy bajos. El osciloscopio de rayos catódicos se usa también para hacer mediciones de voltaje, ya que la inclinación del haz de electrones es proporcional al voltaje aplicado a las placas o electrodos del tubo.
3. ¿Cómo se genera el voltaje?
Un aparato o dispositivo que suministra energía eléctrica recibe el nombre de fuente de fuerza electromotriz, o simplemente fuente de f.e.m.. La fuerza electromotriz es la magnitud que caracteriza el comportamiento del generador en un circuito eléctrico. Este dispositivo convierte la energía química o mecánica, en energía eléctrica. Con frecuencia, se emplean las iniciales f.e.m. para designar esta magnitud, que siendo una energía se la denomina impropiamente fuerza. Según su definición la f.e.m. se expresará en unidades de energía partido por unidades de carga. Este es también el caso de las magnitudes potencial y diferencia de potencial. Por tal motivo su unidad en el SI es el volt. Una fuente de f.e.m.. realiza trabajo sobre la carga que pasa por él elevando la energía potencial de la carga . Una batería ideal es una fuente de f.e.m.. que mantiene una diferencia de potencial constante entre sus dos terminales, independientemente del flujo de carga que existe entre ellos. En una batería real la diferencia de potencial entre los bornes, denominada tensión de bornes, no es igual al valor de la f.e.m.. de la batería. Así pues, una batería real puede considerarse como una batería ideal mas una pequeña resistencia r denominada resistencia interna de la batería.
PRÁCTICA DE LABORATORIO #1
INTRODUCCIÓN
Un circuito es la combinación de varios elementos unidos en puntos terminales que proporciona al menos una trayectoria cerrada por la cual puede fluir una carga. El flujo de carga que atraviesa cualquier material encuentra una fuerza opuesta que, en muchos aspectos, es similar a la fricción mecánica. Esta oposición se denomina resistencia del material; es provocada por las colisiones entre los electrones y entre éstos y otros átomos en el material, las cuales convierten la energía eléctrica a calor. La unidad de medida de resistencia es el ohm, cuyo símbolo es la letra griega omega. La resistencia de cualquier material con un área transversal uniforme se determina mediante los cuatro factores siguientes:
1. El material 2. La longitud 3. El área transversal 4. La temperatura.
Los materiales elegidos, con su singular estructura molecular, reaccionan en forma diferente de las presiones para establecer corriente a través de él. Los conductores que permiten un flujo de carga generoso con poca presión externa tendrán niveles de resistencia bajos, en tanto que los aisladores tendrán características de resistencias altas.
Como podría expresarse, entre más carga pase por la trayectoria, más alto es el nivel de resistencia, en tanto que cuanto más grande es el área, más baja es la resistencia. En consecuencia, la resistencia es directamente proporcional a la longitud e inversamente proporcional a la longitud e inversamente proporcional al área.
MATERIAL UTILIZADO
a) Porta pilas b) 4 Pilas. c) 1 foco de 6 volts. d) Socket e) Juego de caimanes.
f) Resistencias de: OHMS WATTS
10 1/2
220 1/2
470 1/2
1000 1/2
4700 1/2
10,000 1/2
DESARROLLO
Colocamos el porta pilas al multímetro mediante las terminales. y observamos la pantalla indicadora del multímetro. Tenemos como medición 3.04 volts, y en el foco 2.07. Haciendo más mediciones encontramos que 130.65 mili Amperes.

Verificar el valor de las resistencias mediante los códigos de colores.
a) amarillo, violeta, café, oro. 470 OHMS +/- 5%.
b) Café, rojo, rojo, oro. 1200 OHMS +/- 5%.
c) Café, negro, naranja, oro. 10, 000 OHMS +/- 5%.
Valor aproximado Valor real
470 478.2 OHMS y 472.06 OHMS
1200 1.185 Kilo OHMS y 1.180 Kilo OHMS
10000 9.983 Kilo OHMS y 10.267 Kilo OHMS
10 10.59 OHMS y 10.5
220 218.04 OHMS y 217.2 OHMS
100000 102.52 Kilo OHMS y 103.5 Kilo OHMS
10 000 9.968 Kilo OHMS.
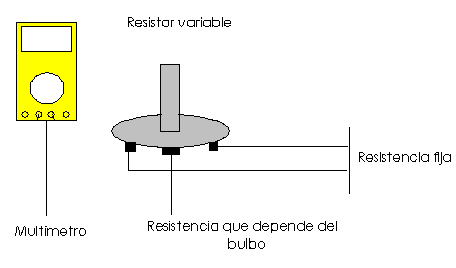
Con el resistor variable, el porta pilas y el multímetro vamos a construir un circuito cerrado en el cual por medio del resistor regulemos el paso de corriente y todo ello será medido por el multímetro. Veamos el siguiente diagrama.
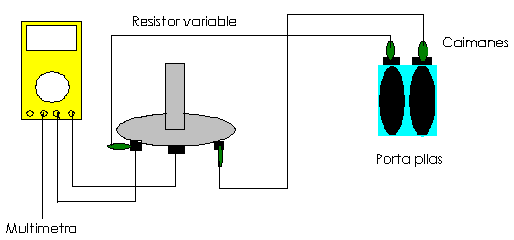
CONCLUSIONES
Antes de realizar esta práctica tenía muchas interrogantes acerca de la electricidad, sus formas de medición, los dispositivos para hacerlo, las diferentes herramientas que se necesitan para realizar un circuito, entre otras cosas que poco a poco mediante avanza el curso iré aprendiendo.
Es de vital importancia que un ingeniero tenga una idea clara todo lo relacionado con la electricidad debido que forma parte de su naturaleza y su desarrollo profesional. En la vida diaria podemos observar fenómenos eléctricos desde encender un foco por el cual pasa la energía eléctrica y la transforma en energía luminosa, también por ejemplo el movimiento de los electrones en un conductor y el análisis de desplazamiento de los 10 cms instantáneos, entre otras cosas. Algunos de los materiales utilizados resultaron ser familiares pero el a usarlos mas a fondo llegan a ilustrar y a proporcionar grandes ideas para el desarrollo y proyectos dentro de mi carrera.
BIBLIOGRAFÍA
Análisis de circuitos lineales
Boylestad
Prentice Hall
CAPITULO 2
SECCIÓN 2.1
1. Encuentre la fuerza de atracción en Newtons entre las cargas Q1= 1 micro Coulombs y Q2 = 2 micro Coulombs.
a) r= 1 m. (90X109N.m2/C2)(2X10-6C)(2X10-6)/1 F = 0.036 N.
b) r = 10 m. (90X109N.m2/C2)(2X10-6C)(2X10-6)/100 F = 3.6X10-4 N.
c) r = 3 m. (90X109N.m2/C2)(2X10-6C)(2X10-6)/9 F = 4X10-3 N.
2. Determine la distancia entre dos cargas de 20 micro Coulombs si la fuerza entre las dos cargas es 3.6X104 N.
F = KQ1Q2/r2 r2 = (9X109N.m2/C2)(20X10-6C)(20X10-6C)/3.6X104 N
r2 = 1X10-4 r = raíz 1X10-4 m2 r= 0.01 m.
SECCIÓN 2.2
1. Encuentre la corriente en amperes si pasan 650 C de carga por un alambre de 50 s.
I = Q/t I = 650 C/50 s I = 13 Amperes.
2. Si pasan 465 C de carga por un alambre en 2.5 minutos, encuentre la corriente en amperes.
I = 465/150 = 3.1 Amperes.
3. Si existe una corriente de 40 A para 1 minuto ¿Cuántos Coulombs de carga han pasado por el alambre?
I = Q/t Q = It Q = (40 A) (60 s) q = 2400 Coulombs.
SECCIÓN 2.3
1. ¿Cuál es el voltaje entre dos puntos si se requieren 96 mJ de energía para mover 50X108 electrones entre ellos?
V = W/Q V = (96X10-3J)/(50X108) V = 1.92 X 10 -11 Volts.
2. Si la diferencia de voltaje entre 2 puntos es 42 V ¿Cuánto tabajo se requiere para llevar 6 C de un punto a otro?
W = QV W = 6 C X 42 Volts W = 252 Joules
3. Encuentre la carga Q que se necesita para mover 96 J de energía a través de una circunferencia de voltaje de 16 V.
Q = W/V Q = 96/16 Q = 6 C
SECCIÓN 2.4
1. ¿Cuánta corriente proporcionará teóricamente una batería con un valor nominal Ah de 200 durante 40 h?
Vida (horas) = Valor nominal A - hrs. (Ah)/ Amperes descargados (A)
Amperes descargados = Valor nominal / Vida (horas)
200/40 = 5 Amperes
2. ¿Cuál es el valor nominal Ah de una batería que proporciona 0.8 A durante 76 h?
Valor nominal = Vida (hrs.) (Amperes descargados)
= (76 Horas) (0.8 A) = 60.8 Ah.
SECCIÓN 2.5
1. Analice las propiedades de la estructura atómica del cobre que lo hagan buen conductor.
El número de electrones que posee el cobre en la última capa es de uno, con lo que se requiere menos energía para moverlo lo que permite el flujo de la corriente más fácilmente y un movimiento casi instantáneo de los mismos al hacerle pasar una corriente eléctrica.
2. Explique los términos aislante y voltaje de conducción.
Aislante: Son todos aquellos materiales en los cuales debe aplicarse un voltaje muy alto para producir un flujo que corriente que se puede medir.
El voltaje de conducción: es la diferencia presente de potencial que para por un determinado conductor.
SECCIÓN 2.6
1. ¿Qué es un semiconductor?
Es un material que tiene un valor de conductividad entre el de un aislante y el de un conductor. Es muy importante en la fabricación de dispositivos electrónicos semiconductores.
2. ¿Qué es un conductor?
Son materiales que permiten un flujo generoso de electrones con una aplicación muy pequeña de voltaje.
3. ¿Qué es un aislante?
Son materiales en los cuales debe aplicarse un voltaje muy alto para producir un flujo de corriente que se pueda medir.
SECCIÓN 2.7
1. Si un amperímetro lee 2.5 A durante un periodo de 4 minutos, determine la carga que ha pasado por el medidor.
I = Q/t Q = It Q = (2.5A)(240 s) Q = 600 C.
2. ¿Cuáles son las diferencias importantes en la forma como se conectan los amperímetros y los voltímetros?
El voltímetro se conecta principalmente desde la fuente de energía o de alguna resistencia que se encuentre dentro del circuito y la diferencia con el amperímetro se puede conectar desde cualquier punto del circuito.
CAPITULO 3
SECCIÓN 3.2
1. ¿Cuál es la resistencia de un alambre de cobre de 200 ft de longitud y 0.01 pulgadas de diámetro (T = 20 ºC).
R = l / A R = (10.37 CM OMHS/ft)(200 Ft)/ 100 CM
Acm = (dmil)2 = (10 mil)2 R = 20.74 OHMS
2. ¿Cuál es el área en mil circulares de un conductor de aluminio de 80 ft de longitud con una resistencia de 2.5 OHMS?
R = l/A A= l/R A = (17.0)(80 ft) / 25 OHMS A = 544 CM
1 CM ------- 3.1416/4 mil2
544 ------- X = ? 427.25 mil.
SECCIÓN 3.3
1. La resistencia de un alambre de cobre es de .92 OHMS a 4 ºC ¿A qué temperatura será a 1.06 OHMS?
236 ºC + 4 ºC = 236 ºC + t2
0.92 OHMS 1.06 OHMS
t2 = 1.06 OHMS (240 ºC/0.92) - 236 ºC = 90.5 ºC.
¿A qué temperatura será 0.15 OHMS?
236 ºC + 4 ºC = 236 ºC + t2
0.92 OHMS 0.15 OHMS
t2 = (0.15OHMS) (240 ºC/0.92 OHMS) - 236 ºC = -196.8
SECCIÓN 3.4
1. Usando unidades métricas, determine la longitud de un alambre de cobre que tiene una resistencia de 0.2 OHMS y un diámetro de 1/10 pulgadas.
R = l/A L = (R) (A) L = (0.2 OHMS) (1/20)
L = 0.01 pulgadas
2. Determine el ancho de un resistor de carbono que tiene una resistencia laminar de 150 OHMS si la longitud es 1/2 pulgadas y la resistencia es 500 OHMS.
R = L / A A = L / R A = (150) (1/2) / 500
A = 0.15 Pulgadas.
SECCIÓN 3.5
1. La resistencia de un alambre de cobre es 2 OHMS a 10 ºC ¿Cuál es su resistencia a 60 ºC?
Resistencia del Alambre de cobre es de 234.5
234.5 ºC + 10 ºC = 234.5 ºC + 60 ºC
2 R2
R2 = 2.16 OHMS
SECCIÓN 3.8
1. Encontrar el rango en el cual debe existir un resistor que tiene las siguientes bandas de colores para satisfacer la tolerancia del fabricante.
a) Verde (5) Azul (6) Naranja (X103) Dorado +/- 5 = 56 Kilo OHMS +/- 5%.
b) Rojo (2) Rojo (2) Café (X101) Plateado +/- 10% = 220 OHMS +/- 10%
c) Café (1) Negro (0) Negro (X100) = 10 OHMS
2. Encontrar el código de colores para los siguientes resistores de 10 %.
a) 220 OHMS = rojo, rojo, café, plateado.
b) 4700 OHMS = Amarillo, violeta, rojo, plateado.
c) 68 Kilo OHMS = Azul, Gris, Naranja, Plateado.
d) 9.1 M OHMS = Blanco, Café, Azul, Plateado.
SECCIÓN 3.9
Encuentre la conductancia de cada una de las resistencias siguientes:
a) 0.086 OHMS
G = 1/0.086 = 11.62 Siemens.
b) 4 Kilo OHMS
G = 1/4000 OHMS = 2.5 X 10 -4 Siemens.
c) 2.2 Mega OHMS
G = 1/2.2X10 6 = 4.54 X 10 - 7 Siemens.
CAPITULO 4
SECCIÓN 4.1
1. ¿Cuál es la caída de voltaje a través de un resistor de 6 OHMS si la corriente que pasa por él es de 2.5 A?
E = (I)(E) E = (2.5)(6OHMS) E = 15 Volts.
2. ¿Cuál es la corriente que pasa por un resistor de 72 OHMS si la caída de voltaje a través de el es de 12 Volts?
I = E/R I = 12V/72OHMS = .166 Amperes.
3. ¿Cuánta resistencia se requiere para limitar la corriente a 15 mA si la caída de voltaje en el resistor es de 6V?
R = E/I R = 6 V/15X10-3 A = 400 OHMS.
4. En el arranque ¿Cuál es el consumo de corriente en la batería de un automóvil de 12 V si la corriente del motor que se enciende es de 0.056 OHMS?
I = E/R I = 12V/0.056OHMS = 214.28 Amperes.
SECCIÓN 4.2
1. Trace las curvas lineales de un resistor de 100 OHMS y 0.5 OHMS.
2. Trace las características de un dispositivo que tiene una resistencia interna de 20 OHMS de 0 V a 10 V y una resistencia interna de 2 OHMS para voltajes mayores.
SECCIÓN 4.3
1. Se disipan 420 J de energía mediante un resistor en 7 minutos. ¿Cuál será la energía que irá al resistor?
P = W/t P = 420 J/420 s P = 1 Watt.
2. La energía para un dispositivo es de 40 Joules por segundo (J/s). ¿Cuánto tiempo se requerirá para proporcionar 460 J?
P = W/t t = W/P t = 460 J/s/40 J t = 11.5 s.
SECCIÓN 4.5
1. ¿Cuál es la eficiencia de un motor que tiene una salida de 0.5 hp con una entrada de 450 W?
Eficiencia = Salida de energía / Entrada de energía.
Eficiencia = 373 Watts / 450 Watts = (0.82)(100) = 82 %.
2. El motor de una sierra eléctrica tiene una eficiencia determinada de 68.5 %. Si se requieren 1.8 hp para cortar una pieza de madera particular. ¿Cuál es la corriente obtenida de una toma de corriente de 120 V?
.685 = (1.8)(746 W) / Pi Pi = (1.8)(746 W/hp) / .685 = 1960.29 W.
I = 1960.29 W / 120 V = 16.33 A.
SECCIÓN 4.6
1. ¿Cuánta energía eléctrica en kilo watts hora se requiere para mantener funcionando un motor de 230 W de una caldera que consume petróleo durante 12 horas semanales en 5 meses?
Energía (KW/h) = energía eléctrica (W) X tiempo (h) / 1000
Energía KW/h = (230 W) (240 h) / 1000
Energía KWh = 552 KWh
2. ¿Cuánto tiempo puede estar encendido un calefactor de 1500 W antes de usar mas de 10 KW/h de energía eléctrica?
tiempo = Energía (KW/h) / Energía eléctrica W
2. ¿Cuánto tiempo puede estar encendido un calefactor de 1500 W antes de usar más de 10 KWh de energía eléctrica?
tiempo = Energía KW/h / Energía eléctrica W
tiempo = 10 000 W/h / 1500 W = 6.66 h.
PRÁCTICA DE LABORATORIO #2
INTRODUCCIÓN
Un circuito esta formado por cualquier cantidad de elementos unidos en los puntos terminales, proporcionando cuando menos una trayectoria cerrada por la cual puede fluir una carga.
Dos elementos están en serie si:
1. Sólo tienen una terminal en común.
2. El punto común entre los dos elementos no está conectado a otro elemento que transporte corriente.
La corriente es la misma que pasa por los elementos en serie, es decir, la corriente I que pasa por cada resistor es igual a la que proporciona la batería. El hecho de que la corriente sea la misma que pasa por los elementos en serie se usa con frecuencia como una trayectoria para determinar si dos elementos están en serie o para confirmar una conclusión.
Una ramificación de un circuito es cualquier parte del circuito que tiene uno o más elementos en serie.
La resistencia total de un circuito en serie es la suma de los niveles de resistencia.
MATERIAL UTILIZADO
1. Un protoboard. 5. Resistencias de (10, 220, 470, 1200, 10,00, 100,000)
2. Multímetro.
3. Juegos de caimanes.
4. Porta pilas con 4 pilas de 1.5 V.
DESARROLLO
Primeramente nos dedicamos a analizar la estructura del protoboard para así poder proseguir en el desarrollo de la práctica. Observamos que posee 64 filas y columnas que van de la letra A a la J, todo ello como un sistema de coordenadas que nos va a permitir identificar cada uno de los puntos y evitar que nos perdamos en el mismo.
Mediante una tabla realice un circuito en donde sea capaz de tomar el valor medido y el valor codificado de tres pares de resistencias. Es muy importante que las resistencias sean equivalentes para poder observar de mejor manera el fenómeno.
TABLA DE RESULTADOS #1
OHMS Valor codificado Valor medido Resistencia total (medida) (calculado)
(R1) (R2) (R1) + (R2)
R1 + R2 10 - 220 9.92 - 216.23 226.37 230
R3 + R4 470 - 1200 470.78 - 1178 1651.4 1670
R5 + R6 10,000 - 100,000 9966 - 102,580 112,450 110,000
TABLA DE RESULTADOS #2
R1 + R2 + RA RA Calculada = 470 Ohms. RA Medido = 470.78 Ohms.
10 + 270 + 470 RT Calculada = 700 Ohms. RT Medido = 698.3 Ohms.
R3 + R4 + RB RB Calculada = 10,000 Ohms. RB Medido = 9.996 Ohms.
470 + 1200 RT Calculada = 470 + 1200 + 10,000 = 11,670 Ohms. RT Medida = 11624 Ohms.
R5 + R6 + RC RC Calculado = 1200 Ohms. RC Medido = 1.178 Ohms
RT Calculado = 11,200 Ohms. RT Medido = 113,730 Ohms.
TABLA DE RESULTADOS #3
CALCULAR VR1 Y VR2
V1 = (I)(R1) = (.535 mA) (1200 Ohms)= .642 Volts.
V2 = (I)(R2) = (.535 mA) (10,000 Ohms) = 5.35 Volts.
V = (I)(RT) = (.535 mA) (11,200 Ohms) = 5.992 Volts.
RT = 6/11,200 = .535 mA.
Medido Calculado
VR1 .6825 Volts .642 Volts
VR2 5.768 Volts 5.35 Volts.
(VR1 - VR2) 6.449 Volts 5.992 Volts.
Corriente medida Corriente calculada
1 .578 mA .535 mA
2 .578 mA .535 mA
3 .578 mA .535 mA
CONCLUSIÓN
En esta práctica aprendimos a utilizar el protoboard realizar conexiones con éste, llevar a cabo la teoría a la práctica. Analizamos los circuitos en serie, utilizamos el multímetro para realizar los cálculos y utilizamos las fórmulas necesarias para corroborar los cálculos medidos, en los cuales observamos una ligera diferencia, la cual la atribuimos al +/- 5% de tolerancia que poseen las resistencias dentro de un sistema.
Podemos establecer que la práctica se realizó con éxito y se llevó a cabo el objetivo de la práctica.